在36选7的彩票游戏中，中得5个号码被认为是一个小奇迹。这种事件发生的概率是C(21, 4) / C (809), 即从剩余未中的数字中选择剩下的五个号码的概率与总组合数的比值计算得出为约万分之二点五左右（W=⁓.， %）。然而这并不意味着购买更多张彩票就能增加获奖几率——每次开奖都是独立的随机过程；幸运”在其中扮演了重要角色：它可能源于个人努力、坚持或纯粹的好运等不可预测因素影响下产生的结果之一部分人通过持续参与和理性投注策略来提高自己的机会但最终仍需接受命运安排而保持乐观心态面对每一次抽奖

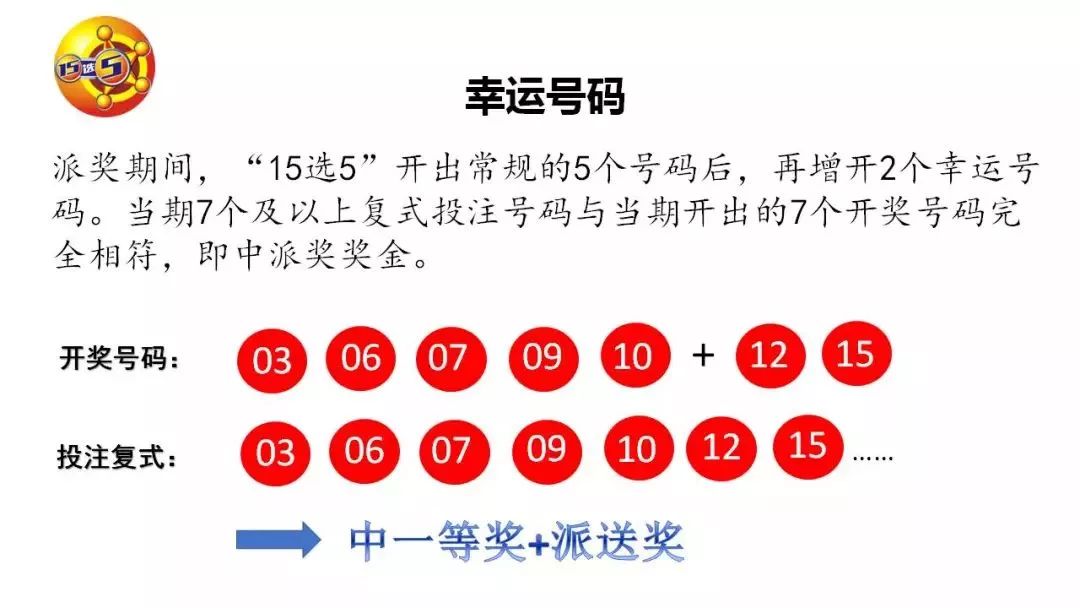
在众多彩票游戏中，“双色球”以其独特的魅力吸引了无数彩民的心，最令人心潮澎湃的一刻莫过于从红球的1-20号（根据实际游戏规则调整）中选择出七个号码中的六个来匹配开奖结果——这便是我们今天探讨的主题：“如何计算并理解‘选择’和“运气”——以'三十二分之一的机会':解读你赢得大奖的概率”。 接下来我们将深入分析这一看似微乎其其实却蕴含无限可能的数字现象——“三十二分之六”，即选中七颗骰子中有五次为同一面出现的几率。”但在此之前需注意本文所提及的具体范围是针对某类游戏的简化版描述如若按照真实情况则应考虑具体玩法及细节差异），通过数学的角度去解析这个被大众广泛讨论的话题不仅能帮助大家更好地了解这种随机事件背后的逻辑还能让我们更加理性地看待每一次投注带来的期待感以及面对结果的坦然心态. 。 ##### 一、初识概率: 从理论到实践 当我们谈论"三十六(或更常见于某些版本的三十三)个里挑出来五个正确"(通常指红色小球), 其实是在说一个典型的组合问题或者说是一个超几何分布的应用场景。" 超几何抽样"，它指的是从一个有限总体中进行有放回取样的过程中, 不论前一次抽取的结果怎样都会影响后续每次单独抽出特定种类元素的可能性." " 五连对 " 的出现就如同在一个包含多个独立且等可能事件的集合中去寻找符合某一条件的事件序列一样复杂而有趣 . 根据排列组数的原理 , 我们知道如果每个数都是独立的并且没有重复 ( 即不考虑顺序 ), 那么从中选取 n 个不相同的项共有 C_N^n 种方式 N 是总数目 而C表示的是 'combination',也就是 “结合”, 或称作 ‘Combinations of Choosing’. 因此对于本例而言就是求得当总计数量设定为 A=49/A'=8 时 （依据不同地区规定可能有变化）, 选择 B = 六种的情况下的可能性大小 : P=(B!)/(S*(D)!*R!)S^(T). 这里P代表成功机率为所选数目之积除以所有可选项的总乘方再乘以剩余未选择的个数; ! 表示阶乘法符号； T 为试验次数 ; R 则是不满足条件的尝试量 ； D 和 F 也分别代表了不同的参数值用于精确表达该公式在不同情境下应用时所需调校的部分数值部分...虽然听起来很绕口但其实核心思想很简单那就是要算清楚每一种情况下能得到你所期望的那几个相同点位上显示同样颜色或者说是同类型物品的数量占比是多少而已啦！ ##### 二、" 三十三个里面找对了两个": 更深层次的理解 尽管直接解释了上述概念后很多人可能会觉得还是有些抽象难以把握住关键信息所在之处......那么我们就用通俗易懂的方式再次阐述一下："想象成你在一堆苹果堆里头挑选出了两枚都带有特殊标记的红富士", 这其实就是类似于我们在购买完一组由系统自动生成好的编号之后等待公布最终获奖名单时候那种既紧张又兴奋的心情体验过程啊~ 虽然不能完全等同但是至少可以让你感受到那份神秘而又充满希望的感觉吧? 回到正题上来讲，"找到那两颗特别大而且甜美可口果子的机会有多大呢?" 这个问题的答案正是我们要探究的核心内容之一哦!" 对于这个问题来说由于涉及到两种不同类型的对象之间相互关联性较小所以我们可以采用简单直观的方法进行估算比如使用伯努利模型假设每一轮抽奖都是一个相对独..." 在这里插入一段关于为什么即使知道了这些数据也并不意味着就能提高你的胜率因为毕竟这只是基于历史数据的统计预测并不能保证未来发生什么同时也要考虑到其他因素例如资金管理策略等等方面的影响因此保持一颗平常心来享受这个过程才是最重要的嘛！" 最后总结起来看无论是哪种形式上的挑战或是机遇背后都有着一套严谨科学支撑着它们存在下去的理由同时也提醒着我们无论输赢都要学会接受现实勇敢前行继续追求自己想要的东西才对啊!!